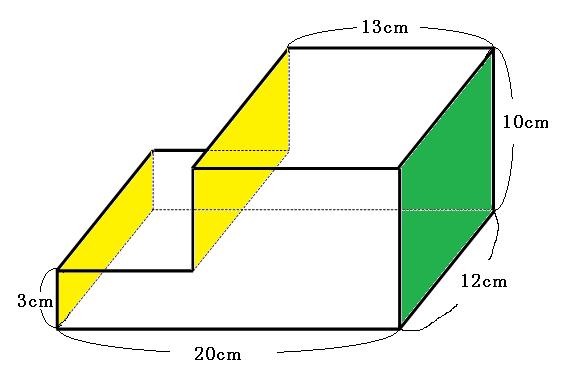
円柱の容積は?1分でわかる意味、求め方と式、表面積の計算、体積と直径の関係 四角柱の体積 四角柱とは下図に示す図形です。底面が台形なので、底面積は台形の面積を計算しましょう。 よって、 四角柱の体積=(35)÷2×4×6=96cm 3 です。 四角柱の体積の公式は?1分でわかる求め方、公式立体は円柱になり,表面積は底面積×2=16 π ×2 (cm 2 )と側面積8 π ×7 (cm 2 )の合計になります 底面積2つで32 π (cm 2 ),側面積56 π (cm 2 )の合計は π (cm 2 ) (答) ※以下,8番以後の問題を解くには,中学校3年生で習う三平方の定理が必要になります.まだ習っ 球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
立体の表面積の求め方
立体の表面積の求め方-立体の表面は、底面と側面から成っており、底面積と側面積の和が表面積になります。 ・底面積\(=1\) つの底面の面積 ・側面積\(=\)側面の面積の総和 ・表面積\(=\)すべての面の面積の和 このように、表面積は、各部の面積の総和になるので、できるだけ 展開図 を利用した方が楽に求められます。立体の表面積展開図(入試問題) → 携帯版は別頁 == 立体の表面積展開図(入試問題) == 要点11 ≪円柱の側面積≫ 円柱の表面積は,2つの底面積と側面積の和になります. 右図のように底面の半径が r ,高さが h である円柱の側面は長方形で,側



1
立体の表面積の求め方や公式をまとめましたが、基本にのっとって丁寧に計算するもよし、公式に当てはめて求めてもよしです。また表面積だけでなく、体積を求める問題とも多く出会うでしょう。問題演習の数をこなして、慣れるのを意識してみてください。 *練習問題の回答* (1)a 三 うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい7立体の体積と表面積 練習問題 ⇨ P 55 115中学の数学幾何I_H_p0357indd 465中学の数学幾何I_H_p0357indd 46 623 PM6129 623 PM 47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積
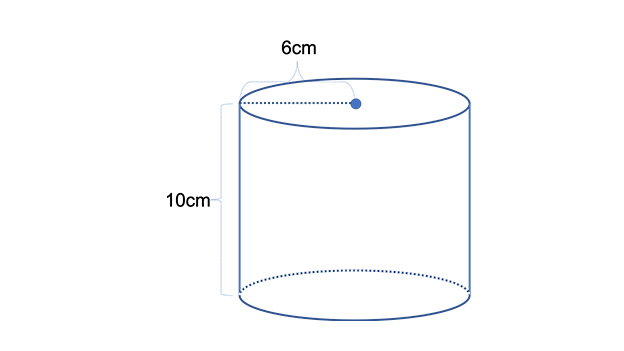
そして円柱の体積は「底面積×高さ」で求めることができるので1256×5= 628㎤ となります。 まとめ いかがだったでしょうか?立体図形の体積の求め方を理屈から理解できたと思います。今回解説したやり方を身につけてお手持ちの問題集や参考書などで 今回は、立方体と直方体の体積の求め方(公式)について書いていきたいと思います。 立方体の体積の求め方公式 直方体の体積の求め方公式 立方体・直方体の体積を求める問題 問題① 《立方体の体積の求め方》 問題② 《立方体の体積の求め方》 問題③ 《直方体の体積の求め方 円柱の表面積の求め方を3ステップで解説していくよ。 3ステップでわかる!円柱の表面積の求め方 例題をときながら円柱の表面積の求め方を勉強していこう。 例題 半径3cm、高さ10cmの円柱の表面積を求めなさい。 つぎの3ステップで求めることができるんだ。 Step1 底面の面積を求め
半径がrの球の中心とその球面上面積がr 2 であるような円形の球面とを結んでできる円錐状の、立体の頂点部分の開き具合。球面全体は4πsrになります。 これは平面角のラジアンと同じ考え方ですが、立体ですので半径rの球体を考えます。 旅人算の解き方 図形が動いた跡の面積の求め方 図1の直方体4個分の表面積の和と図2の立体の表面積の比は 5:4となりました。 図1 図2 (1)「あ」の長さは何cmですか。 (2)図2の立体を2個作ってぴったり重ね、 上の立体を点Pを中心に45°回転させて、図3のような立 体を作り 立体を切り開いた図のこと ・柱体の表面積 底面積×2+側面積 (側面積=柱体の高さ×底面の周りの長さ) ・角錐の表面積 底面積+側面積 (側面積=合同な二等辺三角形×4) ・円錐の側面のおうぎ形の中心角 半 径 母 線 360 × 半 径 母 線




中1数学 立体の表面積 例題編 映像授業のtry It トライイット




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
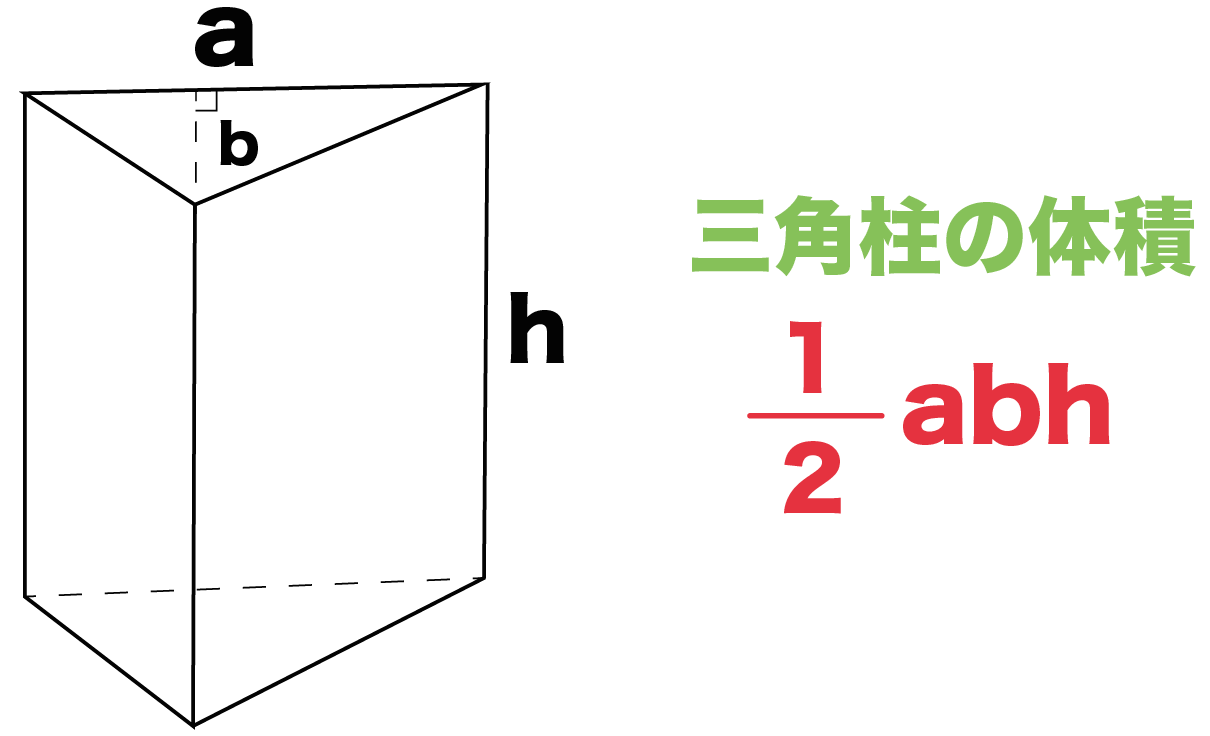
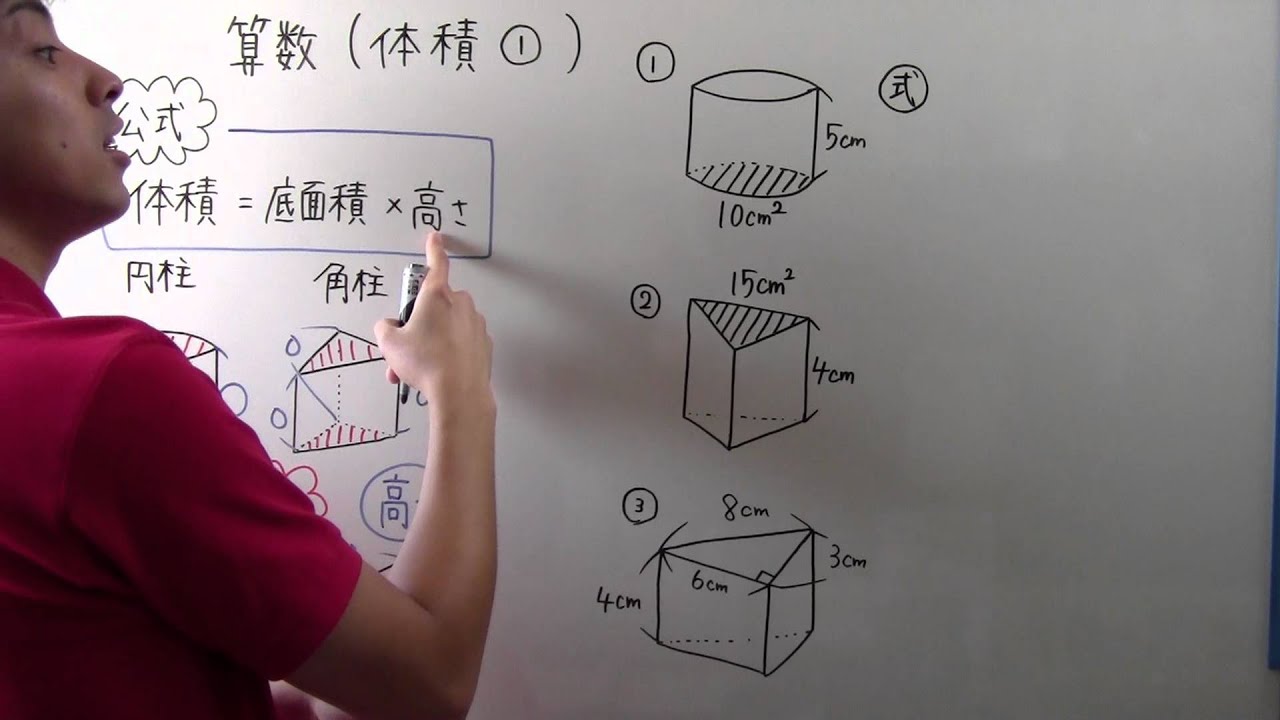
面積を求める例題 まずは面積を求める例題から説明します。面積を求めるときのポイントは どのような線が集まって面を形成しているか をイメージすることが大切です。 三角形 下の図のように\(y=x\)の直線があり、原点,\((1,0)\),\((1,1)\)の3点を結ぶ三角形の面積\(S\)を求めてみたいと思います。 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle 続いて、三角柱の表面積の公式は「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた$8cm^2$ですね。 側面積の求め方ですが「高さ × 底面の周の長さ」で求めることができます。 底面の周の長さは「5cm,4cm,4cm」と出ているので足して13cm。



一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋
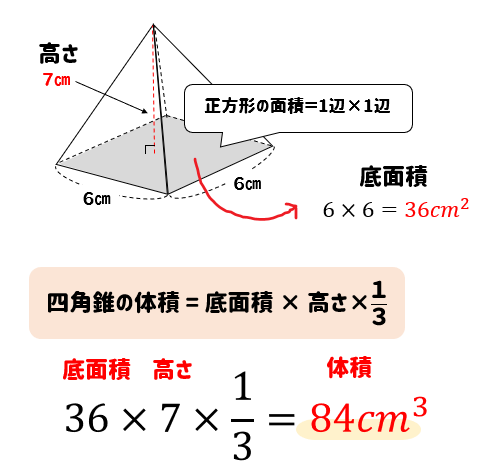



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題球の表面積を求める公式は、S = 4πr^2 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
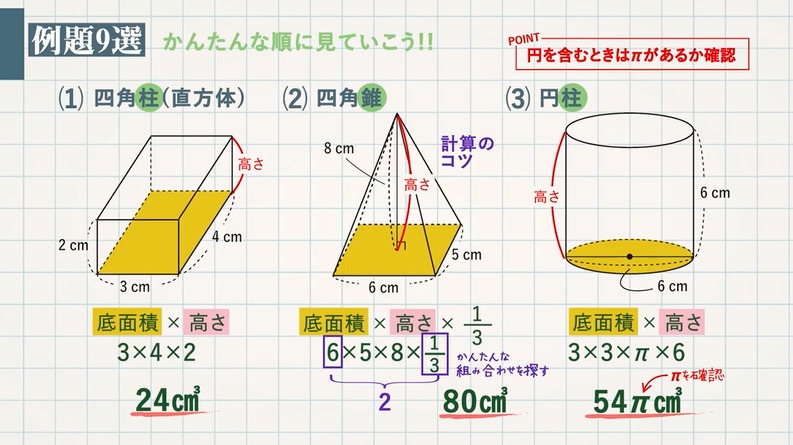
楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り Sm^2球面の表面積、Rm半径 ということになります。 今回の公式を導出するポイントは球の表面積Sm^2 を求めることです。 考え方 この定義式からどのようにしてω=2π(1cosθ)が出てくるのかを説明します。 先ほどの図を正面から2次元的に見るとこんな2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方




6年算数角柱と円柱の体積 立体の体積 教え方
ゾウの表面積の求め方 45 ( 6807 × 身長 ) ( 7073 × 前足の太さ ) なんでこんな式になるんでしょうか? 特に最初の45は一体何なのか鼻? さっぱり分かりませんが、とにかくこれが公式だそうです。 なぜこんな公式があるのかと言えば、 薬の量を




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




角錐 円錐の体積と表面積の公式 数学fun
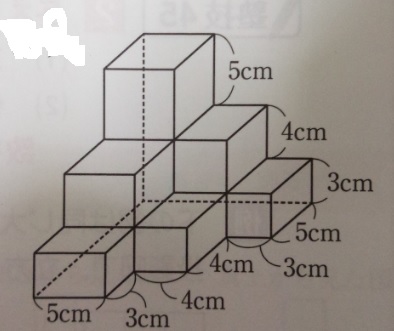



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法



円錐とは 体積 表面積の公式や求め方 受験辞典




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学
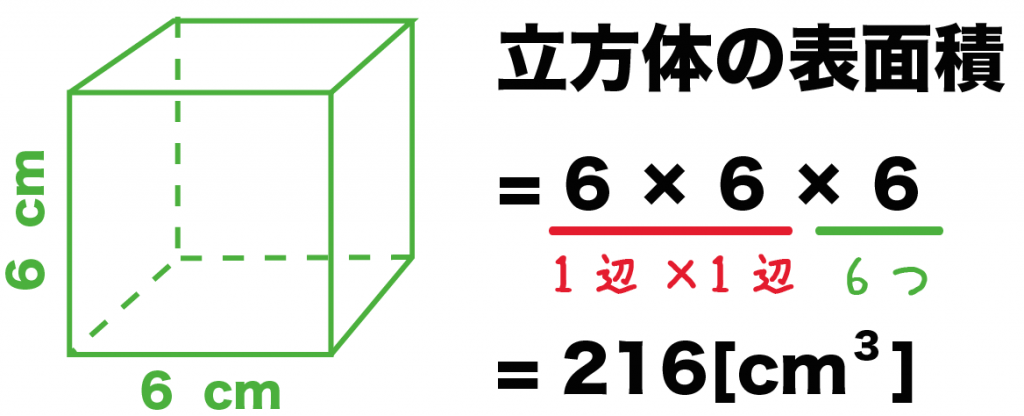



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円柱の表面積 Youtube




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
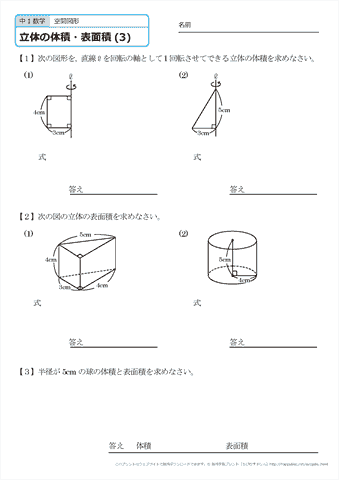



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




スタディピア 立体の表面積




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト
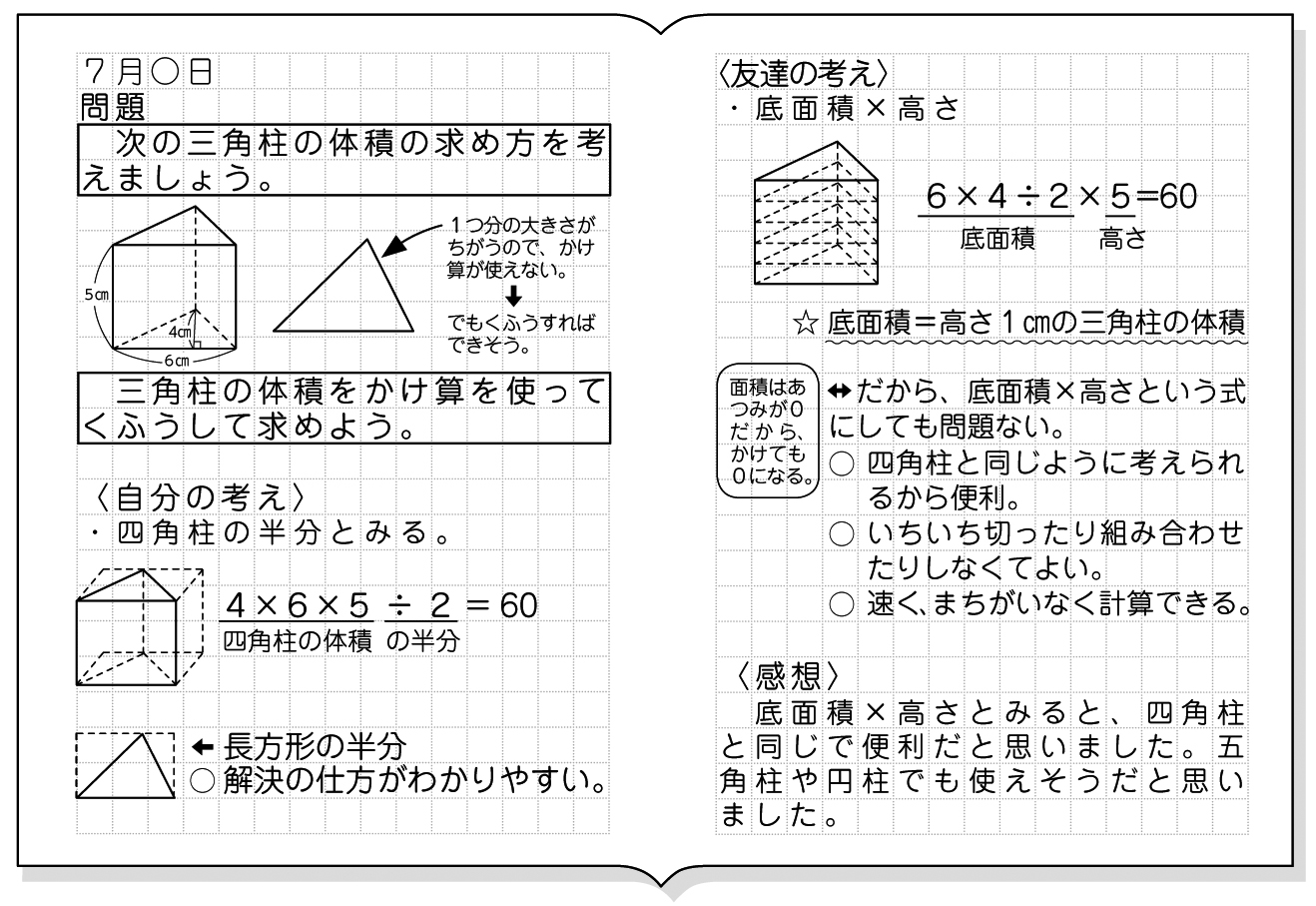



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術




中1 数学 中1 立体の表面積 Youtube




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム



円柱の表面積の求め方




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook
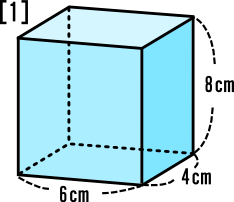



中学1年数学練習問題 立体 円錘 三角錘等 の表面積の求め方と解答




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
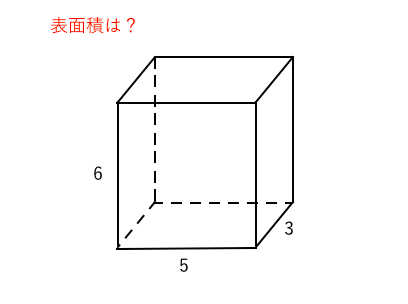



表面積のすべて 苦手な数学を簡単に



表面積 の求め方まとめ 立体ごとの違いやポイントをチェック お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




スタディピア 立体の表面積




球の表面積と体積の公式 数学fun




体積の求め方 立方体 長方体 小学生 算数のノート Clearnote




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



この立体の表面積の求め方を教えて下さい まずは 赤の直方体の表面積1 Yahoo 知恵袋



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



立体の表面積




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか



1




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




小5 算数 小5 3 直方体と立方体の体積 Youtube




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく



小6 算数 小6 25 体積 円柱 角柱 Youtube




スタディピア 立体の表面積




中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clearnote




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




表面積の求め方 計算公式一覧




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座
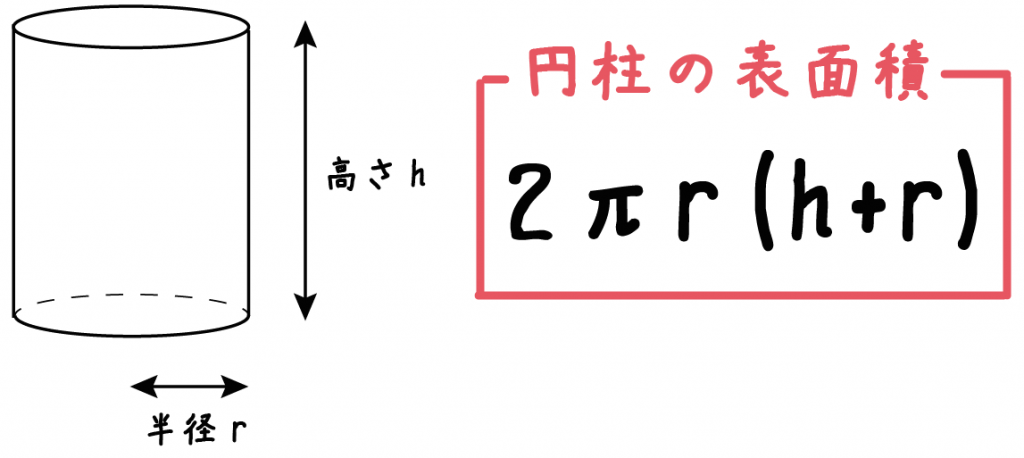



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clearnote




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



直方体の表面積の求め方は 1分でわかる計算 公式と例題




小5 複雑な立体の体積 直方体 日本語版 Youtube




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor
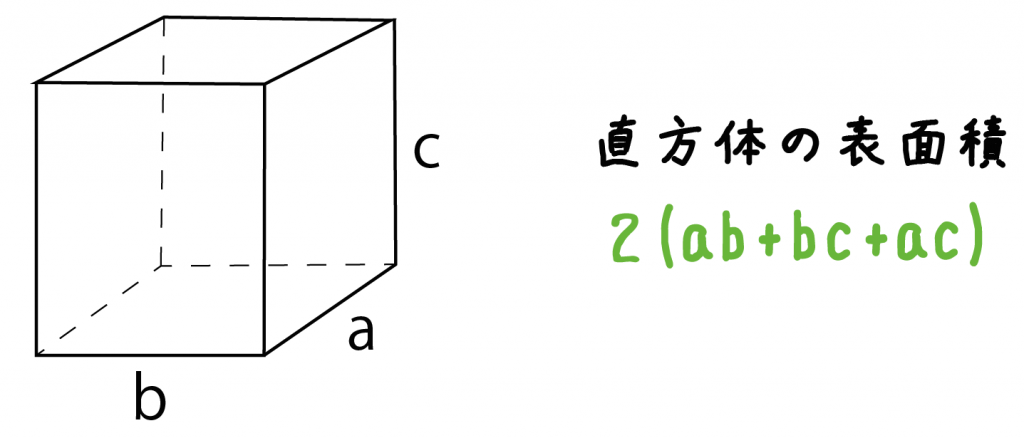



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
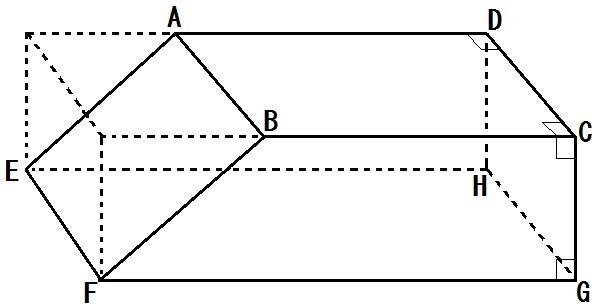



中学数学 空間図形 体積の問題のコツ




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1
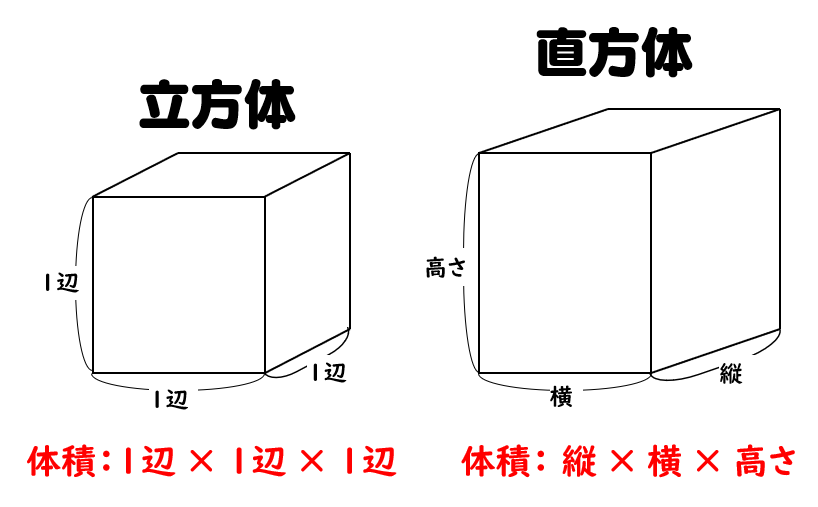



立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
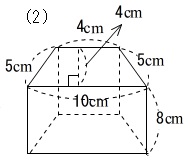



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球




円柱の表面積と体積を求める公式 具体例で学ぶ数学
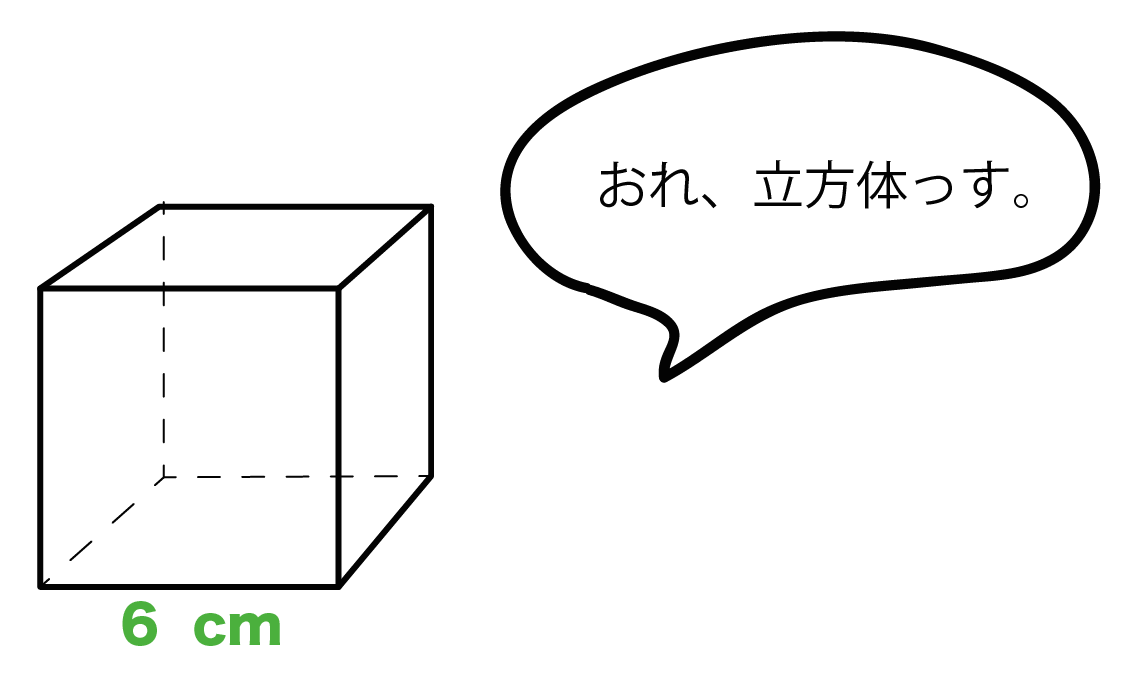



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




中1 数学 中1 立体の体積 Youtube
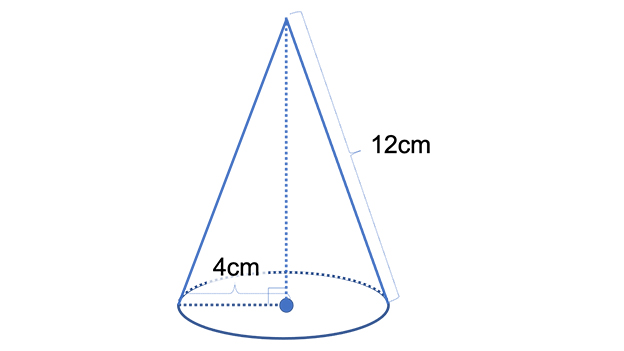



表面積 の求め方まとめ 立体ごとの違いやポイントをチェック お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
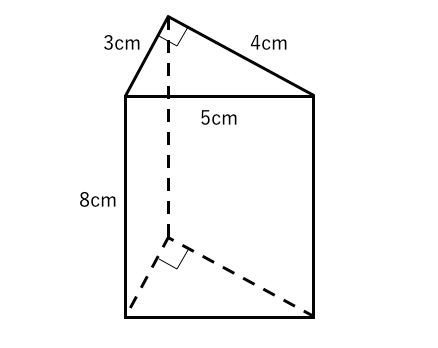



立体の表面積を求める 練習問題 苦手な数学を簡単に




2 を途中式を含めて教えてください Clearnote




角柱 円柱の表面積と体積の公式 数学fun




中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clearnote




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



1




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方



写真の底面が扇形の立体の表面積の求め方を教えてください 特に側面積が Yahoo 知恵袋




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 立体の表面積 について 空間図形 ひっそりと物理や数学を解説する




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




表面積 の求め方まとめ 立体ごとの違いやポイントをチェック お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



0 件のコメント:
コメントを投稿